Modell 2

Radiellt grundvattenflöde till en cirkulär anläggning i ett grundvattenförande poröst lager med öppna magasinförhållanden och en vattengenomsläpplig botten.

Förutsättningar

1. Inflödet till anläggningen sker via två zoner där flödet i Zon 1, Q₁ (L³/T), är horisontellt och radiellt riktat mot anläggningens vägg medan flödet i Zon 2, Q₂ (L₃/T), är axel-symmetriskt riktat mot anläggningens botten. Gränsen (randen) mellan de två zonerna är horisontell och sammanfaller med nivån på anläggningens botten. Inget vattenflöde antas ske tvärs randen.
2. Den hydrauliska konduktiviteten i Zon 1 är isotrop och lika med K₁ (L/T) medan den hydrauliska konduktiviteten i Zon 2 är anisotrop där K_2h (L/T) är den hydrauliska konduktiviteten i horisontalled och K_2v (L/T) den hydrauliska konduktiviteten i vertikalled.
3. Flödet i Zon 1 antas balanseras av grundvattenbildning, W (L/T). Saknas uppgift om grundvattenbildningen får man pröva att ansätta olika värden. Att anta att grundvattenbildningen är lika med nettonederbörden, det vill säga W = (P − E), där P (L/T) är nederbörden och E (L/T) är evapotranspirationen, ger ett mindre influensområde än om man antar att W < (P − E).
4. Om botten i anläggningen är vattenfylld antas att vattendjupet i anläggningen, d (L), är 0 ≤ d ≤ h_a.
5. Om anläggningens form är mer rektangulär än cirkulär kan man approximativt använda radien för en ekvivalent cirkel, r_eq(L), se ekvation (1.7) och Illustration figur 1.7.

Ekvationer

2.1

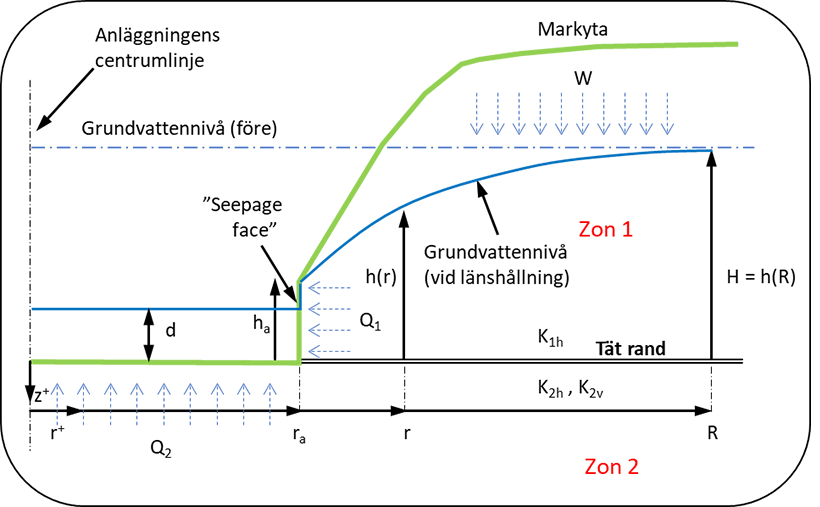
\[H^{2}-h\frac{a}{2}=\frac{Q_{1}}{\pi K_{1}}ln \left ( \sqrt \frac{{\frac{Q_{1}}{\pi We}+\frac{r_{a}^{2}}{e}}}{r_{a}} \right )\]

2.2

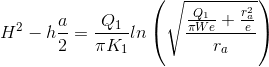
\[R=\sqrt{\frac{Q_{1}}{\pi W}+{r_{a}}^{2}}\]

2.3

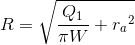
\[h_{1}\left ( r \right )=\sqrt{h_{a}^{2}+\frac{Q_{1}}{\pi K_{1}}\left ( r^{2}-r_{a}^{2} \right )}\]

2.4

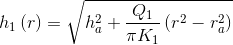
\[m=\sqrt{\frac{K_{2h}}{K_{2v}}}\]

2.5

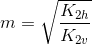
\[Q_{2}=4r_{a}\left ( \frac{K_{2h}}{m} \right )\left ( H-d \right )\]

2.6

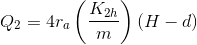
\[h_{2}\left ( r, z \right )=H-\frac{2\left ( H-d \right )}{\pi }sin^{-1} \left \{ \frac{2r_{a}}{\sqrt{\left ( r-r_{a} \right )^2}+\left ( mz \right )^2+\sqrt{\left ( r+r_{a} \right )^2}+\left ( mz \right )^2} \right \}\]

Beräkningsgång

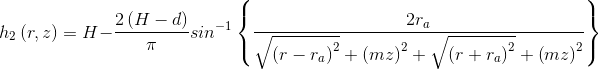
För att kunna beräkna influensavståndet i Zon 1, R (L), måste först ekvation (2.1) lösas rekursivt med avseende Q₁. En ansats kan vara att bortse från eventuella källsprångsytor och maximera storleken på inflödet respektive influensradien genom att ansätta h_a = 0, men som ett känslighetsfall även föra ett resonemang kring att ett högre värde på h_a (på grund av källsprång och/eller eventuellt tätande åtgärder), vilket ger ett lägre inflöde och en mindre influensradie.

Avståndet R från anläggningens centrum till opåverkade grundvattennivåer beräknas sedan enligt ekvation (2.2).

Grundvattenytans nivå på olika avstånd från anläggningens centrum i Zon 1, h₁ (r) (L), beräknas med ekvation (2.3), som även kan användas för att beräkna avståndet till medgivet gränsvärde för grundvattennivåsänkning.

Inflödet över bottenarean, Q₂, beräknas med ekvationerna (2.4) och (2.5).

Grundvattennivån på olika avstånd och djup från anläggningen i Zon 2, h₂ (r, z) (L), beräknas med ekvation (2.6). Om mäktigheten på Zon 2 är tunn kan ekvation (2.6) ifrågasättas. Man antar som regel att influensavståndet i Zon 1 är det som är viktigast för att bestämma påverkansområdet.